利用MSI设计组合逻辑电路
post on 27 Aug 2018 about 1944words require 7min
CC BY 4.0 (除特别声明或转载文章外)
如果这些文字帮助到你,可以请我喝一杯咖啡~
预习报告
内容一:74LS138 相关
逻辑真值表
| $S_2$ | $S_1$ | $S_0$ | $Y_0$ | $Y_1$ | $Y_2$ | $Y_3$ | $Y_4$ | $Y_5$ | $Y_6$ | $Y_7$ |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | $\overline{G_1}$ | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | $\overline{G_1}$ | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | $\overline{G_1}$ | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | $\overline{G_1}$ | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | $\overline{G_1}$ | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | $\overline{G_1}$ | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | $\overline{G_1}$ | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | $\overline{G_1}$ |
由真值表列出逻辑表达式,并化简(这里表达式比较简单,无需使用卡诺图,下同)
$Y_0=\overline{S_2}\,\overline{S_1}\,\overline{S_0}\,\overline{G_1}$
$Y_1=\overline{S_2}\,\overline{S_1}\,S_0\,\overline{G_1}$
$Y_2=\overline{S_2}\,S_1\,\overline{S_0}\,\overline{G_1}$
$Y_3=\overline{S_2}\,S_1\,S_0\,\overline{G_1}$
$Y_4=S_2\,\overline{S_1}\,\overline{S_0}\,\overline{G_1}$
$Y_5=S_2\,\overline{S_1}\,S_0\,\overline{G_1}$
$Y_6=S_2\,S_1\,\overline{S_0}\,\overline{G_1}$
$Y_7=S_2\,S_1\,S_0\,\overline{G_1}$
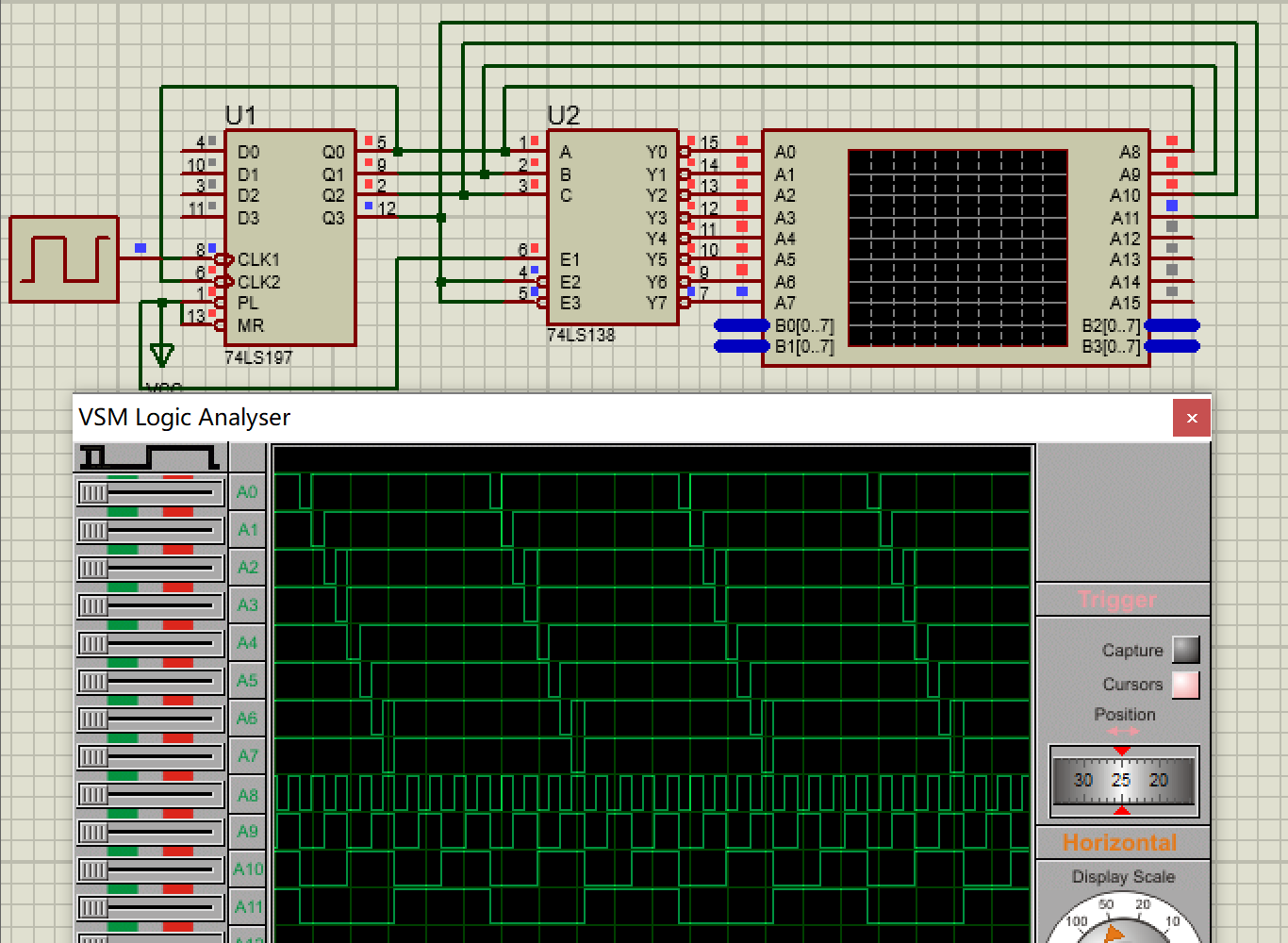
根据上述化简表达式,在 proteus 设计如下电路,并进行仿真
下图中 A0~A7 对应 Y0~Y7 ,A8~A11 对应输入 Q0~Q3 ;连续脉冲的频率为 10kHz。
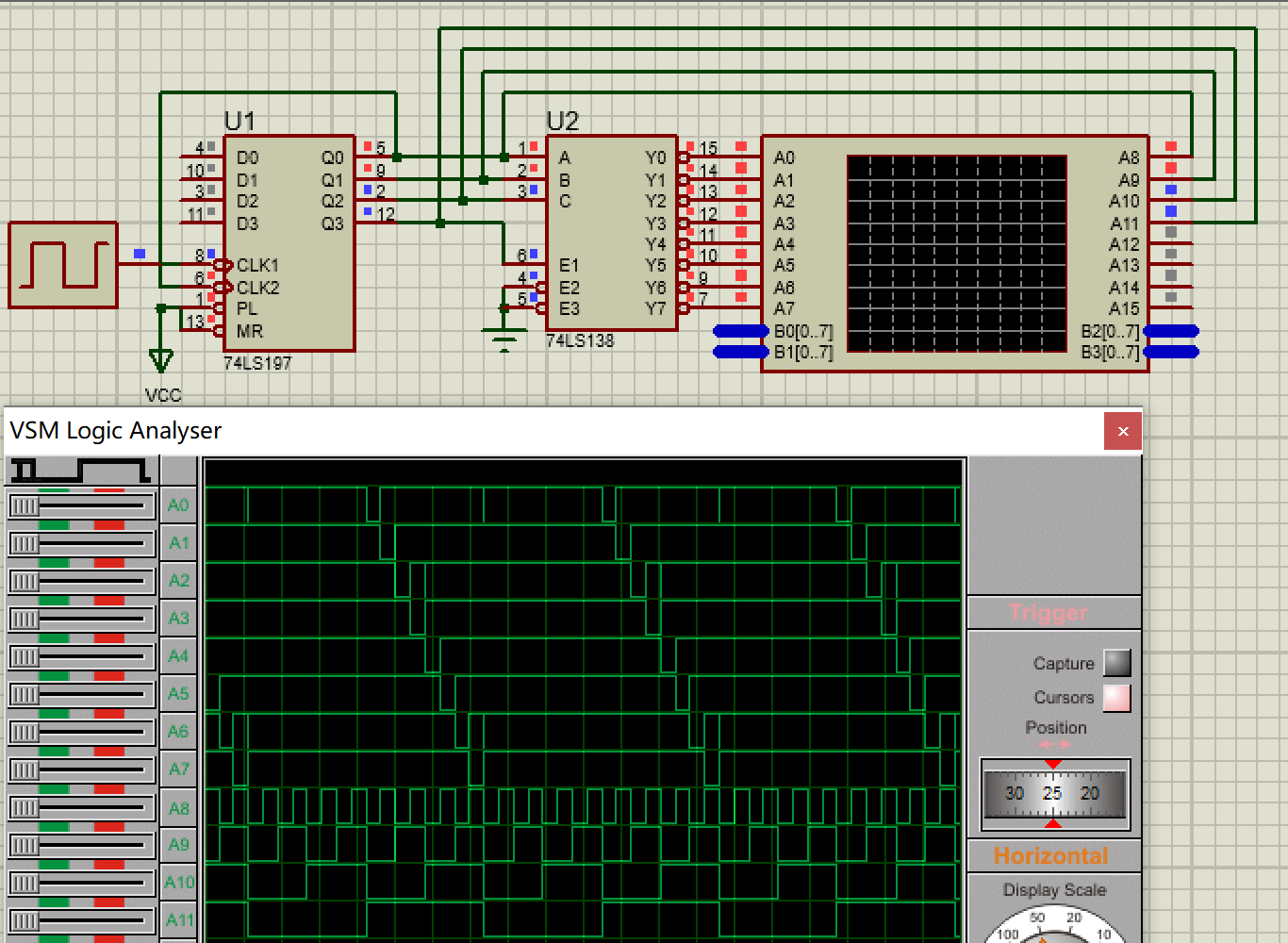
观察对应的波形可以发现,A0~A7 依次慢了一个周期(计数器变化一次),且每十六周期出现一次低电平。
内容二:逻辑单元设计
逻辑真值表
| $M_1$ | $M_0$ | $Y$ |
|---|---|---|
| 0 | 0 | $AB$ |
| 0 | 1 | $A+B$ |
| 1 | 0 | $A\oplus B$ |
| 1 | 1 | $\overline{A}$ |
由真值表列出逻辑表达式,与芯片输出表达式比较得到引脚接法
$S_2 = M_1,S_1 = M_0,S_0 = A,D_1 = D_2 = D_4 = B,D_5 =\overline B ,D_0 = D_7 = 0,D_3 = D_6 = 1,Y = Z $
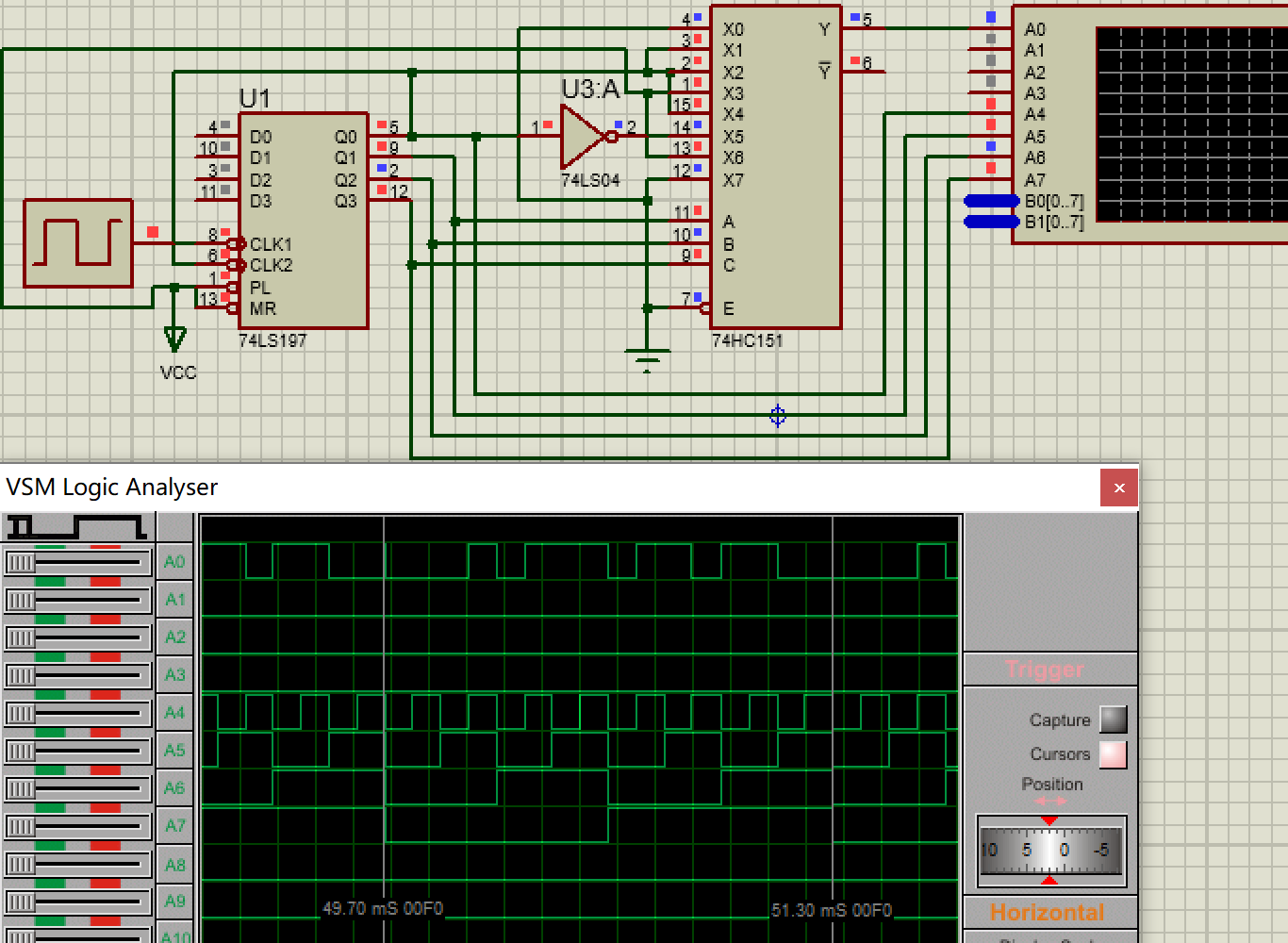
根据上述化简表达式,在 proteus 设计如下电路,并进行仿真
下图中 A0 对应 Y ,A4~A7 对应 B、A、M0、M1 ;连续脉冲的频率为 10kHz。
内容三:算术单元设计,半加半减器
逻辑真值表
| M | A | B | Y | C |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
由真值表列出逻辑表达式,并化简
$Y = \overline{M}\,\overline{A}B +\overline{M}A\overline{B}+ M\overline{A}B + MA\overline{B}= A\oplus B$
$C = \overline{M}AB+M\overline{A}B=(A\oplus M)B$
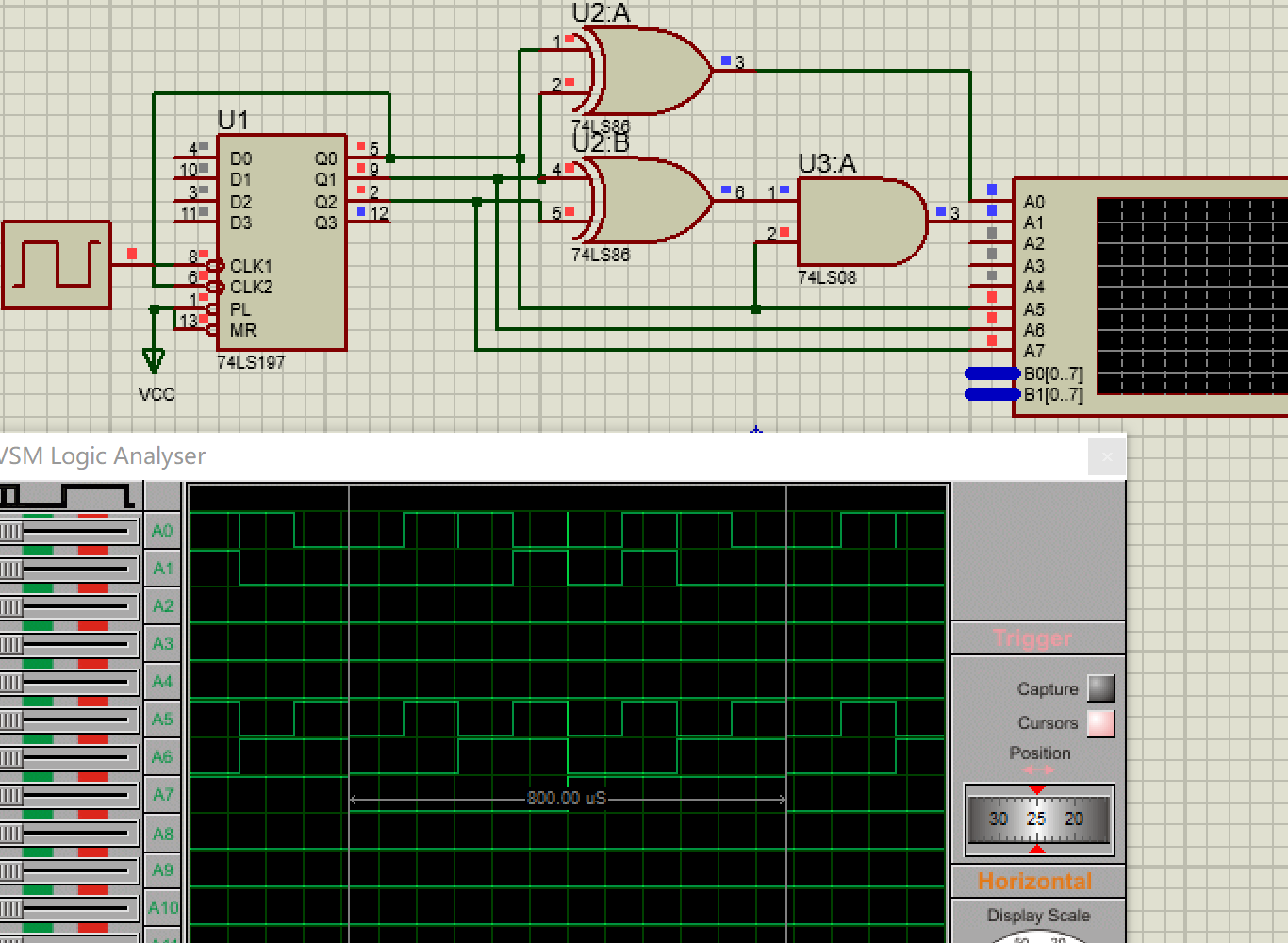
根据上述化简表达式,在 proteus 设计如下电路,并进行仿真
下图中时钟频率为 10kHz,A0 对应 Y,A1 对应 C ,A7、A6、A5 分别对应 M、A、B
可以发现输出 Y、C 的波形与上述真值表中的值相同,符合预期。
实验报告
内容二
实验仪器及器件
数字电路实验箱、万用表、示波器;器件:74LS86 *1、74LS197 *1
代码转换电路设计
具体设计和仿真已在预习报告中完成。
转换电路的效果检验及实验结果分析与讨论
如图,由于实验箱上没有反相器,故使用 74ls86(异或)芯片其中一个输入端接高电平代替。
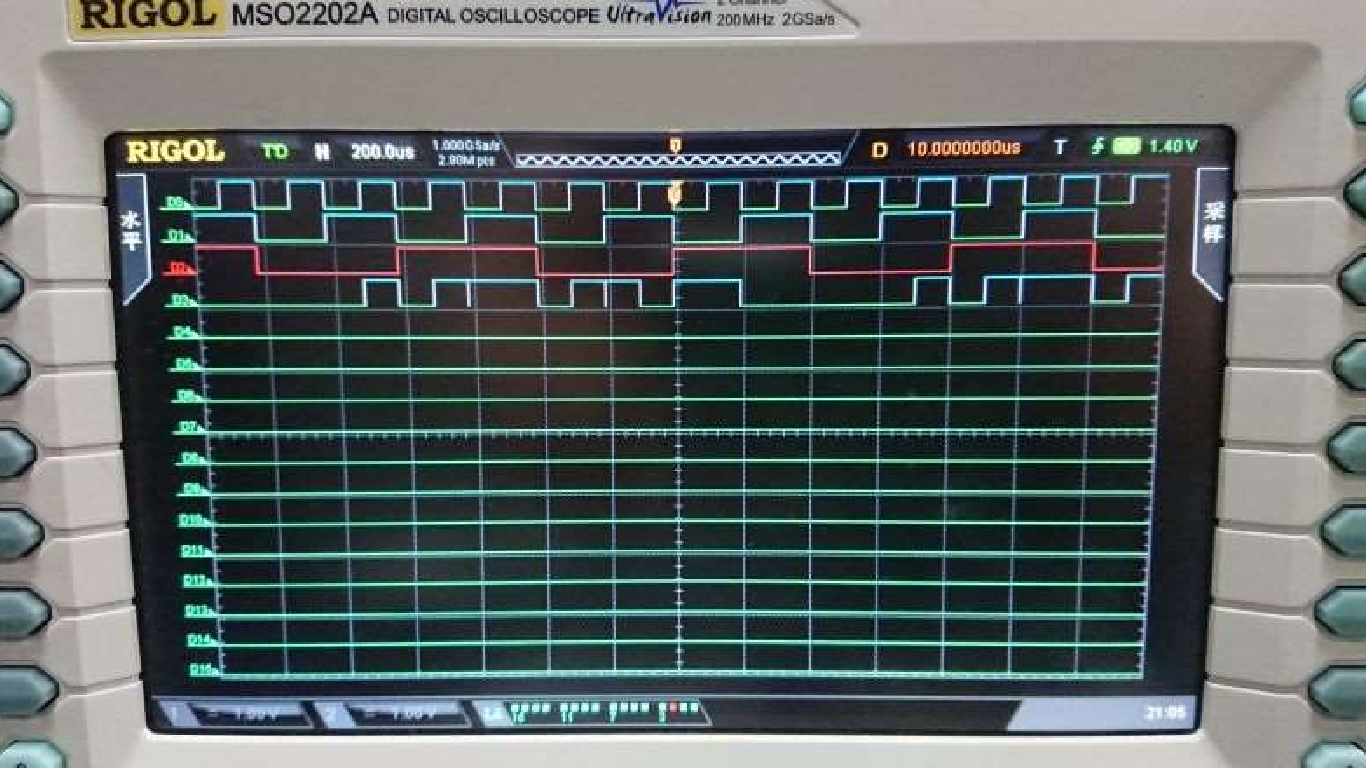
波形图及分析
输入波形 D0~D2(对应 S0~S2)周期依次翻倍,恰按按顺序构成二进制下的 0~15,符合预期;输出波形 D3 中,四个高电平的周期比依次为 1:3:2:2,且各间隔一个周期,符合预期。
烧录到 Basys3 实验板
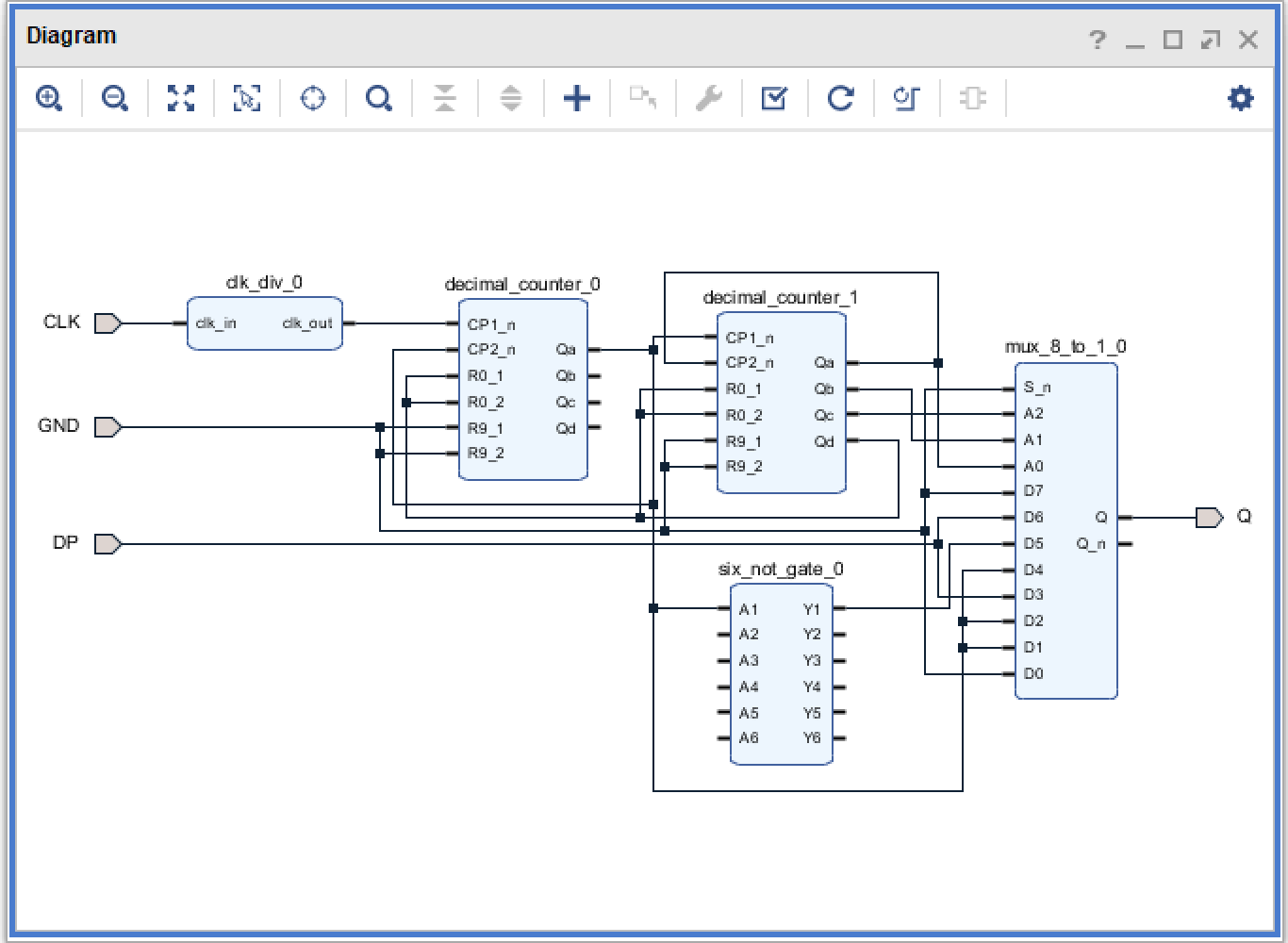
如图,在 Vivado 中设计了实验电路。由于没有 74ls197,在图中使用两片 74ls90 串联成一个十六进制计数 器。并将 CLK 映射到 W5,GND 映射到 R2,DP 映射到 T1,Q(Y)映射到 L1,烧写到板上。
如图,拨动 R2、T1 后,L1 闪烁,且周期比为 1:3:2:2,符合预期。
实验心得与体会
- 通过完成本实验,我基本了解组合逻辑电路的设计与分析过程。
- 预习过程中使用仿真软件对结果进行仿真期间让我对仿真软件有了更深的了解,并学会在找不到原有元 件下如何利用其它元件组合来达到预期效果。
- 实验过程中对示波器的操作应更加熟练,要获得较为稳定的波形,还需要多次练习
Related posts