线性时间求解赋权 Halin 图上的乡村邮差问题
post on 09 Jun 2022 about 4328words require 15min
CC BY 4.0 (除特别声明或转载文章外)
如果这些文字帮助到你,可以请我喝一杯咖啡~
图 $G=(V,E)$,每条边长度 $l(e)$ 为正整数,边集 $E’\subset E$,界 $B$ 为给定正整数。
问:$G$ 中是否有一个圈包含 $E’$ 中的每一条边,并且总长度不超过 $B$?
题目:设计一个多项式时间($O(n)$ 时间)的算法,在赋权 Halin 图上求解乡村邮差问题。
我的求解思路类似于课件中对赋权 Halin 图上的 TSP 问题的求解,此处直接求出图中最短的符合要求的圈,并判断其长度是否超过 $B$(即 $B$ 的取值对本题几乎无影响);一些图也直接借用于课件。设 $H=G=(V,E)$ 是一个赋权 Halin 图,$C$ 是伴随圈,并记 $l(u_i,u_j)$ 为节点 $u_i$ 到节点 $u_j$ 的边长,不存在时 $l(u_i,u_j)=+\infty$;$i=j$ 时 $l(u_i,u_j)=0$。思路上通过归纳方式求解,即先讨论原图是一个轮的情况,再在不是轮的情况下不断对扇进行收缩直至变为轮。
若 $H$ 是一个轮
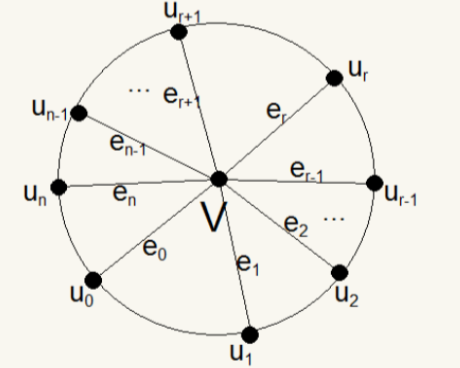
如图,为表述方便记伴随圈 $C$ 上的节点数 $m=n+1$,并记 $r(u_i,u_j)$ 为伴随圈 $C$ 上$u_i\to u_j$ 且不经过 $E’$ 中的边的最长路径。若不存在这样的路径,则 $r(u_i,u_j)=-\infty$。
$E’$ 中不存在 $H$ 的内边
此时有两种走法,一种是只走 $C$ 中的边,不经过中心点 $v$;另一种是经过一次中心点 $v$。则最小圈长为
\[C'=\sum_{k=0}^{m-1}l(u_k,u_{(k+1)\mod{m}})+\min_{i,j\in[0,m),i\ne j}\lbrace 0,l(u_i,v)+l(v,u_j)-r(u_i,u_j)\rbrace\]直接求这个式子是 $O(m^2)=O(n^2)$ 的,接下来使用前缀和的思想将其下降为 $O(n)$ 复杂度。记前缀和(prefix)为 $P$,前缀和前缀最小值为 $P’$,则有
\[P_0=l(u_0,v)\\ P_{i+1}=P_i+l(u_{i+1},u_i)+l(v,u_{i+1})-l(u_i,v)\\ P'_0=P_0\\ P'_{i+1}=\min\lbrace P'_{i},P_{i+1}\rbrace\]记后缀和(suffix)为 $S$,后缀和后缀最小值为 $S’$,则有
\[S_n=l(u_n,v)\\ S_{i-1}=S_i+l(u_{i-1},u_i)+l(v,u_{i-1})-l(u_i,v)\\ S'_n=S_n\\ S'_{i-1}=\min\lbrace S'_{i},S_{i-1}\rbrace\]显然 $P,P’,S,S’$ 都可以通过线性时间求解,于是
\[C'=\sum_{k=0}^{m-1}l(u_k,u_{(k+1)\mod{m}})+\min_{i,j\in[0,m),i\ne j}\lbrace 0,l(u_i,v)+l(v,u_j)-r(u_i,u_j)\rbrace\\ =\min_{i,j\in[0,m),i\ne j}\lbrace l(u_i,v)+l(v,u_j)+r(u_0,u_i)+r(u_j,u_n)\rbrace\\ =\min_{i\in[1,m)}\lbrace P'_{i-1}+S'_i\rbrace\]也可以线性复杂度求解。其他情况下 $C’$ 仍有类似的表达式,可用完全相同的方法线性求解,后文省略。
$E’$ 中有且只有一条 $H$ 的内边
此时必经过非叶节点 $v$,设这条边的两个节点分别为 $v,u_j$。则最小圈长为
\[C'=\sum_{k=0}^{m-1}l(u_k,u_{(k+1)\mod{m}})+\min_{i\in[0,m),i\ne j}\lbrace l(u_i,v)+l(v,u_j)-r(u_i,u_j)\rbrace\]$E’$ 中有且只有两条 $H$ 的内边
此时必经过非叶节点 $v$,设这两条边的两个节点分别为 $u_i,v$、$v,u_j$,不妨假设 $i<j$。则最小圈长为
\[C'=\sum_{k=0}^{m-1}l(u_k,u_{(k+1)\mod{m}})+l(u_i,v)+l(v,u_j)-r(u_i,u_j)\]$E’$ 中有三条或以上 $H$ 的内边
显然这种情况下要多次经过非叶节点 $v$,不存在圈,于是
\[C'=+\infty\]若 $H$ 不是轮
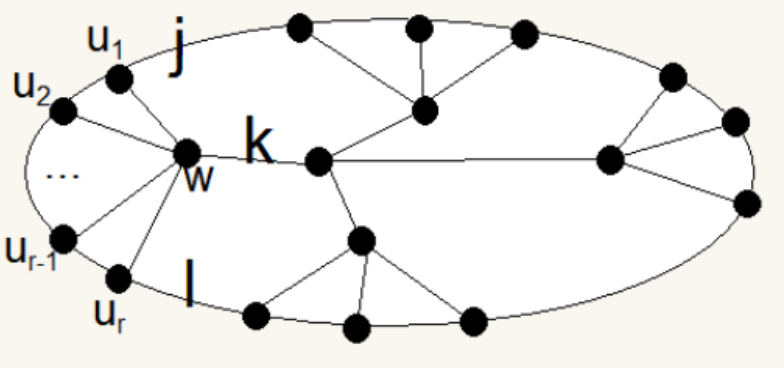
如图,则 $H$ 含有一个扇,记节点 $u_1,\dots,u_r,w$ 及相关的边构成的扇为 $F$,并记 $r(u_i,u_j),1\le i<j\le r$ 为扇 $F$ 上$u_i\to u_j$ 且不经过 $E’$ 中的边的最长路径。若不存在这样的路径,则 $r(u_i,u_j)=-\infty$。
$E’$ 中不存在 $F$ 的内边
$E’$ 中只有部分或没有边在 $F$ 中
显然此时最小圈不可能在 $F$ 内部,收缩扇 $F$ 得到新 Halin 图 $H’$,分别更新 $j,k,l$ 的边长为
\[l'(j)=l(j)+\frac{C_{jk}-C_{kl}+C_{lj}}{2}\\ l'(k)=l(k)+\frac{C_{kl}-C_{lj}+C_{jk}}{2}\\ l'(l)=l(l)+\frac{C_{lj}-C_{jk}+C_{kl}}{2}\]其中
\[C_{jk}=\sum_{k=2}^rl(u_{k-1},u_k)+\min_{i\in[1,r]}\lbrace l(u_i,w)-r(u_i,u_r)\rbrace\\ C_{kl}=\sum_{k=2}^rl(u_{k-1},u_k)+\min_{i\in[1,r]}\lbrace l(u_i,w)-r(u_0,u_i)\rbrace\\ C_{lj}=\sum_{k=2}^rl(u_{k-1},u_k)+\min_{i,j\in[1,r],i<j}\lbrace l(u_i,w)+l(w,u_j)-r(u_i,u_j)\rbrace\]随后递归求解 $H’$ 上包含 $E\cup\lbrace l,j\rbrace$ 的最小圈 $C’{lj}$,同理求出 $C’{jk}$ 和 $C’_{kl}$;由于反复收缩扇最终一定会得到轮,递归次数是有限的。于是原图 $H$ 最小圈为
\[C'=\min\lbrace C'_{jk},C'_{kl},C'_{lj}\rbrace\]注意单次递归需要更新的次数为常数,递归次数是 $O(n)$ 的,因此总求解复杂度仍为 $O(n)$。
$E’$ 中所有边均在 $F$ 中
此时有两种情况:
- 最小圈需要经过 $H$ 中除 $F$ 外其他的边。
- 最小圈在 $F$ 内部。
对于第一种情况,已经在 $E’$ 中只有部分或没有边在 $F$ 中一节讨论过,因此最小圈长为
\[C'=\min\lbrace C'_{jk},C'_{kl},C'_{lj},\sum_{k=2}^{r}l(u_{k-1},u_k)+\min_{i\in[1,r]}\lbrace l(u_i,w)-r(u_i,u_r)\rbrace\rbrace\]注意在前缀后缀预处理后上式可以常数时间求解,递归次数是 $O(n)$ 的,因此总求解复杂度仍为 $O(n)$。
$E’$ 中有且只有一条 $F$ 的内边
设这条边的两个节点分别为 $w,u_i$,此时最小圈可能不在 $F$ 内部,收缩扇 $F$ 得到新 Halin 图 $H’$,分别更新 $j,k,l$ 的边长为
\[l'(j)=l(j)+\frac{C_{jk}-C_{kl}+C_{lj}}{2}\\ l'(k)=l(k)+\frac{C_{kl}-C_{lj}+C_{jk}}{2}\\ l'(l)=l(l)+\frac{C_{lj}-C_{jk}+C_{kl}}{2}\]其中
\[C_{jk}=\sum_{k=2}^rl(u_{i-1},u_k)+l(u_i,w)-r(u_i,u_r)\\ C_{kl}=\sum_{k=2}^rl(u_{k-1},u_k)+l(u_i,w)-r(u_0,u_i)\\ C_{lj}=\sum_{k=2}^rl(u_{k-1},u_k)+\min_{j\in[1,r],j\ne i}\lbrace l(u_j,w)-r(u_{\min\lbrace i,j\rbrace},u_{\max\lbrace i,j\rbrace})\rbrace\]随后递归求解 $H’$ 上包含 $E\cup\lbrace l,j\rbrace$ 的最小圈 $C’{lj}$,同理求出 $C’{jk}$ 和 $C’_{kl}$;由于反复收缩扇最终一定会得到轮,递归次数是有限的。
若 $E’$ 中所有边均在 $F$ 中,还需要考虑最小圈落在 $F$ 内的情况,则有
\[C'=\min\lbrace C'_{jk},C'_{kl},C'_{lj},\\ \sum_{k=2}^{r}l(u_{k-1},u_k)+\min_{j\in[1,r],j\ne i}\lbrace l(u_j,w)-r(u_0,u_{\min\lbrace i,j\rbrace})-r(u_{\max\lbrace i,j\rbrace},u_r)\rbrace\rbrace\]否则原图 $H$ 最小圈为
\[C'=\min\lbrace C'_{jk},C'_{kl},C'_{lj}\rbrace\]注意单次递归需要更新的次数为常数,递归次数是 $O(n)$ 的,因此总求解复杂度仍为 $O(n)$。
$E’$ 中有且只有两条 $F$ 的内边
此时必经过非叶节点 $w$,设这两条边的两个节点分别为 $u_i,w$、$w,u_j$,不妨假设 $i<j$。收缩扇 $F$ 得到新 Halin 图 $H’$,分别更新 $j,l$ 的边长为
\[l'(j)=l(j)+\frac{C_{lj}}{2}\\ l'(l)=l(l)+\frac{C_{lj}}{2}\]其中
\[C_{lj}=\sum_{k=2}^rl(u_{k-1},u_k)+l(u_i,w)+l(w,u_j)-r(u_i,u_j)\]随后递归求解 $H’$ 上包含 $E\cup\lbrace l,j\rbrace$ 的最小圈 $C’_{lj}$;由于反复收缩扇最终一定会得到轮,递归次数是有限的。
若 $E’$ 中所有边均在 $F$ 中,还需要考虑最小圈落在 $F$ 内的情况,则有
\[C'=\min\lbrace C'_{lj},\sum_{k=2}^{r}l(u_{k-1},u_k)+l(u_i,w)+l(w,u_j)-r(u_1,u_i)-r(u_j,u_r)\rbrace\]否则原图 $H$ 最小圈为
\[C'=C'_{lj}\]注意单次递归需要更新的次数为常数,递归次数是 $O(n)$ 的,因此总求解复杂度仍为 $O(n)$。
$E’$ 中有三条或以上 $F$ 的内边
显然这种情况下要多次经过非叶节点 $w$,不存在圈,于是
\[C'=+\infty\]Related posts